You have no items in your shopping cart.
0
You have no items in your shopping cart.
Some slackliners believe that for a given tension the amount of sag subjected to a slackline from a slackliner will remain the same regardless of the type of webbing used. An argument in favor of this theory would state that trigonometry equations dictate sag and not webbing elongation. Others believe that the webbing does play a major role in determining how much sag a slackliner will subject to a line. Supporting arguments include the notion that increased elongation translates to increased length, which translates to increased sag. As I continue, it will become apparent that the true product of slackline sag is, in part, a blend of both of these theories.
To start I must define two terms: in-use tension and standing tension. In-use tension refers to the tension on the anchor when a slackliner is standing on the line. Standing tension refers to the tension on the anchor presented by the tensioning of the pulley system when the slackliner is not standing on the line.
The in-use tension subjected to a slackline anchor is a function of three main parameters: the slackliner’s weight, the amount of sag subjected by the slackliner at a given point, and the length of the line. Three constants exist with regard to these parameters: an increase in the weight of the slackliner yields an increased anchor load, decreased sag yields an increased anchor load and increasing the line length for a given sag yields an increased anchor load. This rule model forms the backbone structure that the first theory explained in the introduction is based off. You can follow the parameters of this model using the calculator posted below.
However, although the above is accurate, one critical parameter that slackliners need to understand is that the mathematical model used to calculate the tension on the line is only relative to the in-use tension. Because we are measuring the anchor load after the webbing has already elongated, anchor load is not a function of webbing elongation following this theory.
Nonetheless, webbing with higher elongation will sag more for a given tension than lower elongation webbing will. Consider a slackliner who steps up on a chain fence and imagine that, clearly, the chain will not stretch. Next, consider the slackliner swaps the chain for an untensioned bungee cord. Clearly, the slackliner would fall to the ground, and the ground would support the majority of the slackliner’s weight. These scenarios form the basis for the second theory expressed in the introduction.
So, how can both theories be right? They can both be right because they reference two different phenomena. The mathematical model references the condition of the line after a slackliner steps on it, and the other theory references the condition of the line before a slackliner steps on it.
The methods applied in this study are quite simple. I started the test by stretching a 103’ milspec line across two trees. I tensioned the line and walked the line a few times to stabilize the line. I then fine-tuned the standing tension to 838 lbf. After, I sat in the middle of the line, I measured the deflection and I measured the average in-use tension. Lastly, I swapped the sample out for the next sample and repeated the test.

I used five webbing types in my study, in order from highest to lowest elongation: milspec tubular (nylon-6 tubular), type-18 (nylon flat), Mantra MKII (polyester flat), Green Magic (polyester flat) and Kevlar (para-aramid flat).

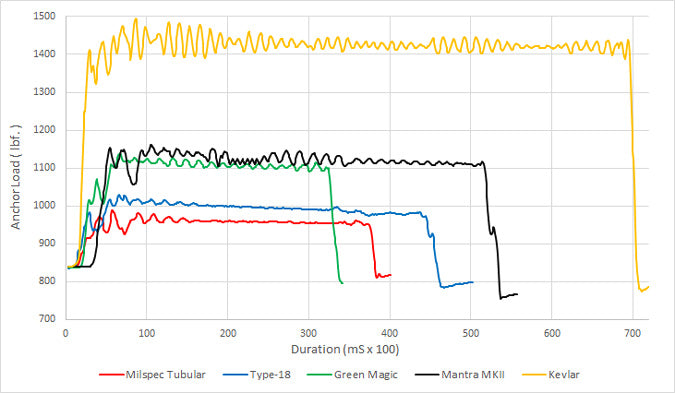
The first graph shows the load experienced by the anchors when subjected to the testing criteria listed above. It is worth noting that high-elongation lines are well able to absorb small load fluctuations caused by wind or other influences whereas low-elongation lines are not. The graph displays this observation clearly.
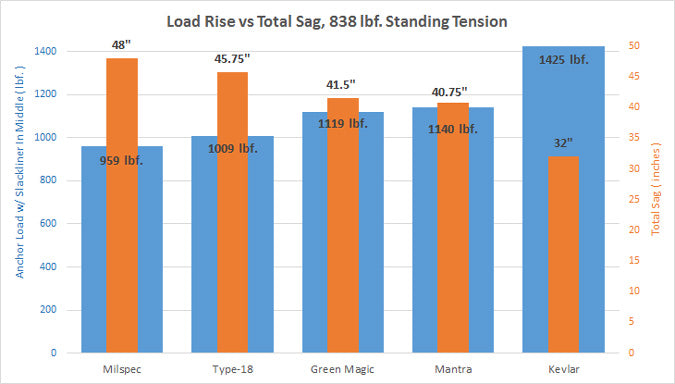
The next graph displays the total sag of the line in relation to the load subjected to the anchors.
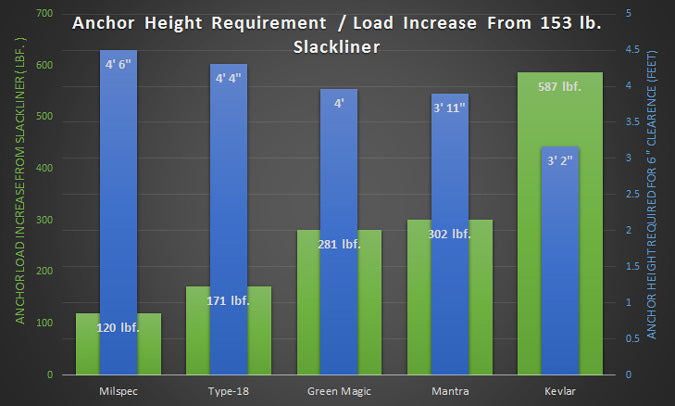
The final graph illustrates the anchor height requirement for a particular webbing type as well as the difference between the standing tension and the in-use tension. Interestingly enough, the in-use tension difference for the milspec tubular line is less than my weight (153 lbs load, 120 lbf increase), but the Kevlar-line increase is 383% of my weight. This information sheds light on why it is ultra-critical to use exceptionally strong components when highlining on polyester or high-tech webbing types.
Low-elongation webbings will produce less sag than high-elongation webbings for a given standing tension, but at the price of increased in-use tension. Overall equal, slackliners can expect to utilize lower-spaced anchors with lower-elongation webbing types.
Written by Sayar Kuchenski
| Product | Price | Quantity | Options | |||||
|---|---|---|---|---|---|---|---|---|
| Features |
| Availability: |
| Price |
| Options |
| Actions |

← Older Post Newer Post →
0 comments